تحليل مسائل تنش و كرنش صفحه اي بر اساس روش هم هندسي مبتني بر تئوري اجزای محدود

حل معادلات ديفرانسيل حاكم بر رفتار يك سيستم از مهمترين مسائلي است كه همواره در زمينه هاي علوم و مهندسي مورد بحث قرار مي گيرد. از آنجايي كه تنها موارد معدودي از اين معادلات را مي توان مستقيما با روش هاي تحليلي حل نمود، روش هاي عددي زيادي در چند دهه اخير براي حل چنين معادلاتي پيشنهاد شده است. روش هاي عددي با ظهور كامپيوترها رشد چشمگيري داشته اند و امروزه به كمك كامپيوترها و اين روش ها قادر به حل معادلات بسيار پيچيده در حوزه هاي متنوع علوم مي باشيم.

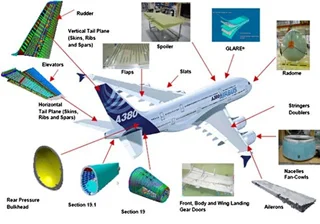
برخي از روش هاي عددي معروف عبارتند از روش تفاضل محدود، روش اجزاي محدود، روش نقاط محدود و روش هاي جديدتر مانند روش هاي بدون مش كه اين روش ها هر يك در پي ديگري آمده و به دنبال ايجاد كارايي، دقت، سرعت بالاتر و ايجاد امكاناتي جديدتر براي حل مسائل و رفع مشكلات روش هاي قبلي بوده اند. از پركاربردترين اين روش ها، روش اجزاء محدود مي باشد كه روشي عددي براي يافتن حل تقريبي بسياري از مسائل مهندسي است. هر چند اين روش براي اولين بار جهت تحليل تنش در سازه هواپيما به كار گرفته شد، ليكن كاربرد آن در بسياري از مسائل مكانيك جامدات، مكانيك سيالات و علوم به سرعت رو به گسترش نهاد. در زمينه مهندسي راه و ساختمان نيز اين روش تحليل سازه هاي بسيار پيچيده و طرح بهينه آنها را به طور موثر و اقتصادي ممكن مي سازد. انگیزه انجام نخستین فعالیت ها در زمینه تحلیل هم هندسی (Isogeometric Analysis) ناشی از شکاف موجود بین دنیای تحلیل اجزاء محدود و مدلسازی کامپیوتری بوده است.

در مراحل ابتدایی، یکی از مهمترین زمینه های تحقیق در تحلیل هم هندسی ایجاد ارتباط بین دو دسته طراحی و تحلیل،‌ و همچنین مشخص سازی موانع و راه حل های ارائه شده موجود در هر دسته بوده است. مسلما یکپارچه سازی تحلیل و هندسه یک مسئله دشوار است و به نظر می رسد که بایستی تغییرات اساسی برای یکپارچگی کامل طراحی مهندسی و فرایندهای آنالیز انجام شود. روش تحلیل هم هندسی در سال ۲۰۰۵ توسط پروفسور هیوز و همکارانش برای رفع نقص های بیان شده، معرفی شد. توابع هندسی محاسباتی زیادی وجود داشتند که می توانستند به عنوان توابع پایه در تحلیل هم هندسی بکار روند. انتخاب بی اسپلاین (B-Spline) و نربز (NURBS) به عنوان پایه اولیه به دلیل پر کاربرد بودن این توابع هندسه محاسباتی در طراحی مهندسی می باشد.

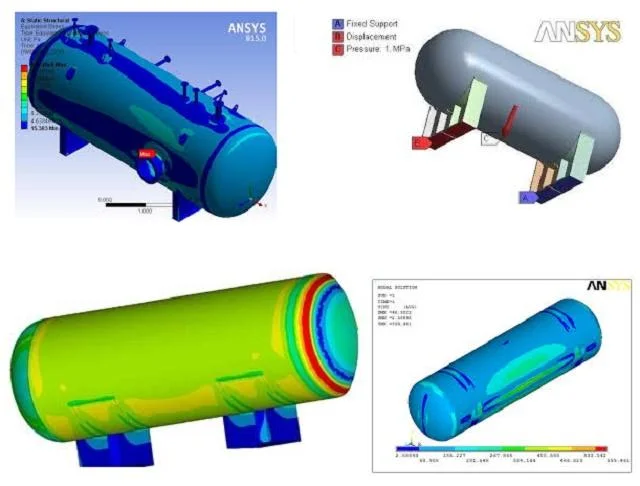
تحليل مسائل تنش و كرنش صفحه اي بر اساس روش هم هندسي مبتني بر تئوري اجزای محدود

ضمن معرفی روش تحلیل هم هندسی و بیان ویژگی های  توابع بی اسپلاین و نربز به عنوان اجزاء اصلی آن، روابط مربوط به تحلیل هم هندسی مسائل تنش و کرنش صفحه ای ارائه شده است. ویژگی بارز این گزارش حل مثالی نمونه بر اساس روابط ارائه شده و چهارچوبی که پیش از این در حل مسائل اجزاء محدود مورد استفاده قرار گرفته بود، می باشد.

تحليل مسائل تنش و كرنش صفحه اي بر اساس روش هم هندسي مبتني بر تئوري اجزای محدود مشتمل بر 4 فصل، 50 صفحه، با فرمت pdf، به زبان فارسی، همراه با ذکر نکات، فرمول های مهم و کاربردی، به ترتیب زیر گردآوری شده است:

فصل 1: مقدمه اي بر تحليل هم هندسي

• مقدمه
• مفهوم تحليل هم هندسي
• مقدمه اي بر تحليل هم هندسي بر پايه توابع نربز

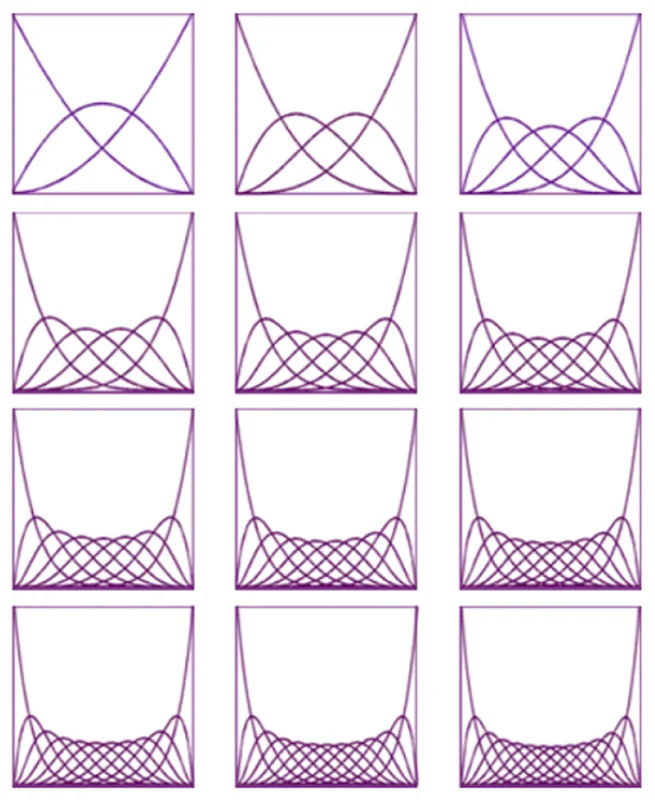
فصل 2: معرفي و بررسي توابع بي اسپلاين و نربز

• مقدمه
• نمايش منحني ها و سطوح
• بي اسپلاين
• بردارهاي گرهي
• توابع پايه
• مشتقات توابع پايه بي اسپلاين
• منحني هاي بي اسپلاين
• سطوح بي اسپلاين
• نربز
• توابع پايه نربز
• مشتقات توابع پايه نربز

فصل 3: تحليل هم هندسي در مسائل تنش و كرنش صفحه اي

• تحليل هم هندسي در مسائل تنش و كرنش صفحه اي
• روابط تحليل هم هندسي در مسائل تنش و كرنش صفحه اي
• انتگرال گيري عددي
• اعمال شرايط مرزي

فصل 4: حل مثال عددي

• مثال عددي: صفحه مستطيل شكل تحت اثر نيروي برشي
• مراجع

جهت خرید آموزش تحليل مسائل تنش و كرنش صفحه اي بر اساس روش هم هندسي مبتني بر تئوري اجزای محدود به مبلغ فقط 20000 تومان و دانلود آن بر لینک افزودن به سبد خرید در پنجره بالا کلیک نمایید.

!!لطفا قبل از خرید از فرشگاه اینترنتی برتر فایل قیمت محصولات ما را با سایر محصولات مشابه و فروشگاه ها مقایسه نمایید!!